We can model the candle's height using the linear function:
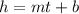
Where
h is the height
m is the slope
t is the time
b is the y-intercept
Given slope = -0.6, we can write:
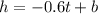
Also given, at t = 11 hours, the height, h, is 22.4 cm. Thus, we can find b:
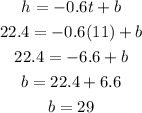
The equation of the candle's height:
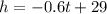
We want to find height of candle after 8 hrs, so we put 8 into "t" of the equation and find the corresponding "h". Shown below:
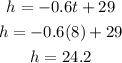
The height, after 8 hrs, was 24.2 centimeters.