Let us use the following variables to represent the total rainfall for the years:

In 2015, the total rainfall in Central City was 13 inches less than the total annual rainfall in Central City in 2000. This can be expressed to be:
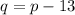
In 2016, the total rainfall in Central City was 33 inches greater than the total annual rainfall in Central City in 2000. This can be expressed to be:
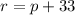
The difference is given to be:
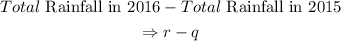
Putting the values we've got, we can calculate the difference to be:
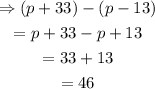
Therefore, the difference in the yearly rainfall from 2015 to 2016 is 46 inches.