Question

PLEASE HELP ME SOLVE THIS PROBLEM I think the table is wrong

Answer 1

Step-by-step explanation:

The question involves getting the expected value or the sum in a deal involving dice

First, we will have to get the probabilities

Probability is defined by

`P=\frac{number\text{ of possible outcomes}}{number\text{ of total outcome}}`

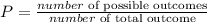
If a six is rolled, the probability will be

`P(6)=(1)/(6)`

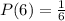
When a 4 or 5 is rolled, the probability will be

`\begin{gathered} P(4\text{ or 5})=(1)/(6)+(1)/(6)=(2)/(6)=(1)/(3) \\ P(4\text{ or 5})=(1)/(3) \end{gathered}`

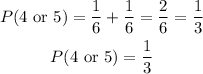
When a 1, 2, or 3 is rolled

`\begin{gathered} P(1\text{ or 2 or 3})=(1)/(6)+(1)/(6)+(1)/(6)=(3)/(6)=(1)/(2) \\ P(1\text{ or 2 or 3})=(1)/(2) \end{gathered}`

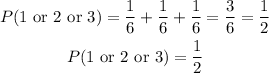
We can now get the expected pay using the relationship

`Expected\text{ pay =x.P\lparen x\rparen}`

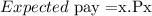
So for rolling a 6, the expected will be

`x.P(x)=\text{ \$}12*(1)/(6)=\text{ \$2}`

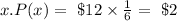
When a 4 or 5 is rolled

`x.P(x)=\text{ \$}6*(1)/(3)=\text{ \$2}`

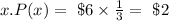
When 1,2, or 3 are rolled

`x.P(x)=-\text{ \$}5*(1)/(2)=-\text{ \$2.5}`

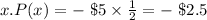
We can now construct the table as follow