Triangular numbers can also be treated as an Arithmetic progression:
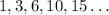
Where the general formula can be given by:
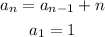
We can check that. for n = 100, we would have:
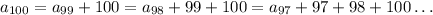
So, to find the 100th number, we must sum all the numbers from 1 to 100. To do so, we use the following formula:

And we find:
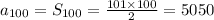
The answer for 9. is 5050.