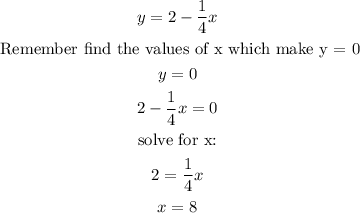A)
In order to find the x-intercepts you need to find the values of x which make:
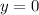
And in order to find the y-intercept you need to evaluate the function for:
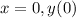
So, for the equation:

The mistake is replace y = 0 in order to find the x-intercept, you need to find the values of x which make the function equal to 0, not replace y for 0.
b.