Question

You roll two regular six-sided dice. Which event is more likely: A. You roll seven (i.e., the dice add up to seven). B. You roll doubles (i.e., both dice show the same number). Show or explain your thinking.

Answer 1

Given:

A regular six-sided dice.

The probability of each number = 1/6

You roll two regular six-sided dice.

If we calculate the probability of the dice add up to seven

The seven will come for the following events

1 + 6

2 + 5

3 + 4

4 + 3

5 + 2

6 + 1

So, the total probability =

`7\cdot((1)/(6))^2=(7)/(36)`

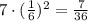
Now, calculate the probability when both dice show the same number

So, the events will be:

1 + 1

2 + 2

3 + 3

4 + 4

5 + 5

6 + 6

So, the total probability =

`6\cdot((1)/(6))^2=(6)/(36)`

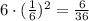
By comparing the results:

`(7)/(36)>(6)/(36)`

So, the answer will be the event that is more like is:

A. You roll seven