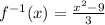Question

Let f(x) = (3x + 9. Find f-'(x).=Vf-'(x) =help (formulas)

Answer 1

Given the function:

`f\mleft(x\mright)=√(3x+9)`

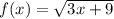
You can find the Inverse Function by following the steps shown below:

1. Rewrite the function using:

`f(x)=y`

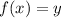
Then:

`y=√(3x+9)`

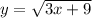
2. Solve for "x":

- Square both sides of the equation, in order to undo the effect of the square root on the right side:

`\begin{gathered} (y)^2=(\sqrt[]{3x+9})^2 \\ y^2=3x+9 \end{gathered}`

- Apply the Subtraction Property of Equality by subtraction 9 from both sides of the equation:

`\begin{gathered} y^2-(9)=3x+9-(9) \\ \\ y^2-9=3x \end{gathered}`

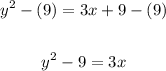
- Apply the Division Property of Equality by dividing both sides of the equation by 3:

`\begin{gathered} (y^2-9)/(3)=(3x)/(3) \\ \\ (y^2-9)/(3)=x \\ \\ x=(y^2-9)/(3) \end{gathered}`

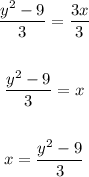
3. Swap the variables:

`y=(x^2-9)/(3)`

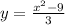
4. Replace the variable "y" with:

`y=f^(-1)(x)`

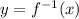
Then, you get:

`f^(-1)(x)=(x^2-9)/(3)`

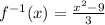
Hence, the answer is:

`f^(-1)(x)=(x^2-9)/(3)`