The general equation of line passing through a point (x, y) can be written as,

Here, m is the slope and b is the y intercept. Th slope can be calculated as,

For two lines to be perpendicular, the slopes will be reciprocal two each other and in opposite sign.
The given lines m is,

The slope is therefore,
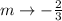
Now, the slope of the line n can be calculated as,

The slope for the line p passing through the pointes (0,3) (3, 4)can be calculated as,

From the calculated slopes, we can infer that the lines m and n are perpendicular to each other.