Question

A truck can be rented from Company A for $50 a day plus $0.70 per mile. Company B charges $20 a day plus $0.80 per mile to rent the same truck. Find the number of miles in a day at which the rental costs for Company A and Company B are the same.At ___? ______ miles, the rental costs are the same

Answer 1

Let's begin by identifying key information given to us:

Truck A = $50 per day + $0.70 per mile

`A=50x+0.7y`

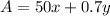
Truck B = $20 per day + $0.80 per mile

`B=20x+0.8y`

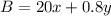
Where x = number of days, y = number of miles

To find the number of miles in a day at which the rental of Trucks A & B are the same, we will have to equate both equations above. We get this:

`\begin{gathered} A=B\Rightarrow50x+0.7y=20x+0.8y \\ 50x+0.7y=20x+0.8y \\ x=1day \\ \text{Substitute the value of x into the equation, we have:} \\ 50(1)+0.7y=20(1)+0.8y \\ 50+0.7y=20+0.8y\Rightarrow0.8y+20=0.7y+50 \\ \text{Putting like terms together, (add '}-0.7y-20^(\prime)\text{ to each side)} \\ 0.8y-0.7y+20-20=0.7y-0.7y+50-20 \\ 0.1y=30 \\ \text{Multiply each side by 10, we have:} \\ 0.1y\cdot10=30\cdot10 \\ y=300miles \end{gathered}`

This therefore, means that at 300 miles, the cost of renting Truck A is the same as renting Truck B