Question

What are the coordinates of the focus of the parabola shown below?y² +16y+ 4x + 4 =0

Answer 1

(14, -8)

Explanations:

The standard equation of a parabola is expressed as;

`y^2=4ax`

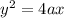
Given the equation of a parabola y² +16y+ 4x + 4 =0

Using the completing the square method

`\begin{gathered} (y^2+16y+((16)/(2))^2)=-4x-4+((16)/(2))^2 \\ (y^2+16y+8^2)=-4x-4+8^2 \\ (y+8)^2=-4x-4+64 \\ (y+8)^2=-4x+60 \\ (y+8)^2=-4(x-15) \\ (y-(-8))^2=4(-1)(x-15) \end{gathered}`

From the result, you can see that the vertex (h, k) is (15, -8) and a = -1

Determine the focus of the parabola

`\begin{gathered} focus=(15+a,-8) \\ focus=(15+(-1),-8) \\ focus=(14,-8) \end{gathered}`

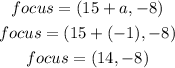
Hence the focus of the parabola is (14, -8)