Answer:
The solutions are -7/2 and 1. Jeffrey is correct.
Explanation:
We have to use the Bhaskara formula to solve this question.
Bhaskara formula:
Suppose we have the following second order equation:
ax² + bx + c = 0
The solution of the equation are:

In this question:
(2x - 1)(x + 3) = 4
We have to apply the distributive property to place the equation in the correct format to apply Bhaskara.
(2x - 1)(x + 3) = 4
2x² + 6x - x - 3 = 4
2x² + 5x - 3 - 4 = 0
2x² + 5x - 7 = 0
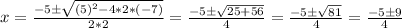
The solutions are:

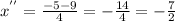
The solutions are -7/2 and 1. Jeffrey is correct.