The mean is also called average. We obtain the mean by finding the sum of the data and then dividing the sum by the number of data.
In the given, we have 6 data with a mean of 118.
Thus, we equate it as follows.
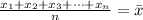
Substitute the value of each given data on the left side and the value of n is 6.
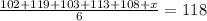
Simplify the numerator.
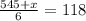
To eliminate the denominator, multiply both sides of the equation by 6.
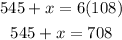
Subtract both sides by 545.
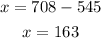
Thus, the value of x must be 163.