There are 650 students graduating from the class, that is 100% of the students.
The class is divided into three groups based on whether or not they are going to attend graduation:
1) 48% of them are attending graduation.
2) 44% of them are not attending.
3) And the rest have not decided yet. (x%)
The three percentages must add up to 100%, so to determine what percentage of the class has not made a decision yet, you have to add the percentages of those who had made a decision and subtract it from 100:

So, 8% of the class has not decided whether or not they are going to attend the graduation.
Now to determine what number of students that 8% represents, you have to calculate the 8% of 650.
For this, multiply 650 by 8 and divide the result by 100:
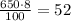
52 students are undecided