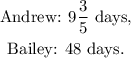Question

Andrew can paint the neighbors house 5 times as fast as Bailey. The year Andrew and Bailey worked together, it took them 8 days. How long would it take each to paint the house. Andrew :Bailey:Please help me solve

Answer 1

Let A be the number of days that Andrew uses to paint the house, and B be the number of days that Bailey uses to paint the house. Since Andrew can paint the house 5 times as fast as Bailey and together take 8 days, we can set the following system of equations:

`\begin{gathered} B=5A, \\ (8)/(A)+(8)/(B)=1. \end{gathered}`

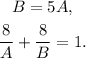
Substituting the first equation in the second one we get:

`(8)/(A)+(8)/(5A)=1.`

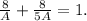
Multiplying the above result by A we get:

`\begin{gathered} ((8)/(A)+(8)/(5A))* A=1* A,_{} \\ 8+(8)/(5)=A\text{.} \end{gathered}`

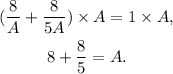
Simplifying the above result we get that:

`A=9(3)/(5).`

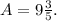
Finally, substituting A=9.6 in B=5A we get:

`\begin{gathered} B=5\cdot9(3)/(5), \\ B=48. \end{gathered}`

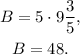
Answer:

`\begin{gathered} \text{Andrew: 9}(3)/(5)\text{ days,} \\ \text{Bailey: 48 days.} \end{gathered}`