Question

A 4 digit number is formed from 1, 2, 3, 4, 5, 6, 7, 8, 9 without repetition. What is the probability of forming a 4 digit even number?

Answer 1

The probability (P) of forming a 4 digit number is

`P=\frac{\text{favorable outcomes}}{possible\text{ outcomes}}=\frac{\#\text{even numbers}}{total\text{ of four digit numbers}}`

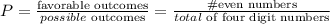
What is the total of four-digit numbers we can assemble with the provided restrictions? Take a look at the following drawing:

In the first digit, we have nine options (all digits are possible); however, after choosing one in the first place, when choosing the second, we can't choose the same as before for repetition is not allowed; then, we have just eight options in the second place. The third and fourth places follow this rule.

Then, the total number of four-digit numbers is

`9\cdot8\cdot7\cdot6=3024`

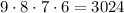
On the other hand, how many of them are even numbers? The idea is similar but changes when analyzing the last (fourth) place. Look at the following drawing:

First, our analysis was made from right to left. A number is even if its last digit is 0,2,4,6, or 8. Zero isn't in the options; then, in order to assemble an even number, we have four options (2,4,6, and 8). After choosing the last (fourth) digit, we have 8 (9-1) options to the third, 7 options to the second, and 6 to the first (actually similar to the before drawing, but in the other direction). Thus there are

`6\cdot7\cdot8\cdot4=1344`

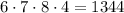
even numbers of them.

Finally,

`P=(1344)/(3024)\approx0.44`

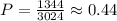
This means that the answer is the last option (0.44).