• Phase shift left ,π/2, units
,
• Vertically ,compressed by a factor of -3 units
,
• Vertically ,shifted up ,4 units
,
• Period of function ,h, is half the period of the parent function
,
• And it has an amplitude of ,3 ,units greater than that of Parent Function.
1) Considering the parent function as y= cos(x) we can examine this one:
y=-3cos(2x-π)+4
y=Acos(B(x+C)) +D General form
2)
0. Notice that we have a ,Vertical Compression, due to factor ,3.
,
1. The Amplitude is ,3 times greater ,than the Parent function for |-3|=3.
,
2. In addition to this, this function was shifted up ,4 units, in comparison to the parent function
,
3. The period is shorter (half than the parent function of cosine function: ,2π) ,since it is ,π
,
4. The ,phase shift to the left ,since it is ,-π,, i.e., ,the ,C, is ,negative,, in comparison to the ,parent function ,and it is given by:
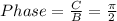
Note that we're considering the general formula y=A(Bx+C)+D
In blue: y=-3cos(2x-π)+4, in red y=cos(x)
3) So the answer is (in order of appearance):
• Phase shift left ,π/2 units
,
• Vertically ,compressed by a factor of -3 units
,
• Vertically shifted up 4 units
,
• Period of function ,h, is half the period of the parent function
,
• And it has an amplitude of 3 units greater than that of Parent Function.