Given
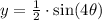
Find
Amplitude and period of the function and graph it.
Step-by-step explanation
the amplitude of the function is the largest value that the given function may attain. the amplitude of the given function is 1/2.
to find the period of the function , divide 2pi by the coefficient of theta
here , the coefficient of theta is 4 .
so , the period =

given function has an amplitude of 1/2 and period of pi/2.
now , we graph the function.
the graph completed one period in the interval
that an effect of shrinking the graph horizontally,
Final Answer
The graph will be made as shown