Given:
Total number of students = 238
Let the number of passing students be x
We're given that 6 times the number of students passed as failed. Hence, the number of students:
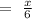
Hence, we can write:

Solving for x:
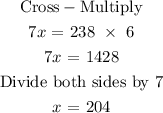
Hence the number of passing students is 204 students
We can find the number of failing students by subtraction:
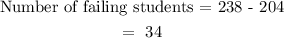
Answer:
Passing students: 204
Failing students: 34