Question

On two investments totaling $9,500, Peter lost 3 % on one and earned 7 % on the other. If his net annual receipts were $169, howmuch was each investment?Step 2 of 2: Solve the system of equations.

Answer 1

From the question

The sum of two investments = $9500

Let one of the investments be $x and the other be $y

Therefore

`x+y=9500--------1`

Peter lost 3 % on one and earned 7 % on the other

Therefore, we say

He lost 3% on $x

That is He lost $0.03x and

He earned 7% on $y

That is He earned $0.07y

Since his net annual receipts were $169

Then we have

`-0.03x+0.07y=169--------2`

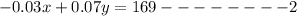
Now we have to solve the equations simultaneously

From the first equation

`x=9500-y------3`

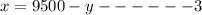
Substitute for x into equation 2

This gives

`-0.03(9500-y)+0.07y=169`

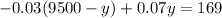
By solving for y we get

`\begin{gathered} -285+0.03y+0.07y=169 \\ -285+0.1y=169 \\ 0.1y=169+285 \\ 0.1y=454 \\ y=(454)/(0.1) \\ y=4540 \end{gathered}`

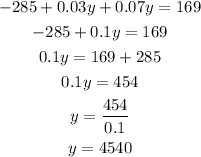
Substitute the value of y into equation 3

This gives

`\begin{gathered} x=9500-4540 \\ x=4960 \end{gathered}`

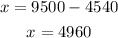
Therefore,

Each investment is

$4960 at 3% loss

$4540 at 7% profit