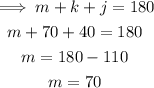Question

Use parallel Lines to find missing angle measure?Find a,i,j,k and m

Answer 1

a=80, i=70, j=40, k=70, and m=70

Explanation:

(a)Angle a and 100° are on a straight line.

The sum of the measures of angles on a straight line is 180 degrees, therefore:

`a+100\degree=180\degree\implies a=180\degree-100\degree=80\degree`

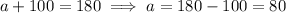
(i)Angle i is a base angle of an Isosceles triangle. Since base angles of Isosceles triangles are equal, we have that:

`i=70\degree`

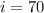
(j)In the triangle:

`\begin{gathered} i+j+70=180\degree\text{ (sum of angles in a triangle)} \\ 70+j+70=180\degree\implies j+140=180\implies j=180-140 \\ j=40\degree \end{gathered}`

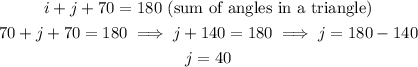
(k)Since lines l3 and l4 are parallel, angles k and 70 degrees are alternate angles. Since alternate angles are equal:

`k=70\degree`

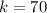
(m)the sum of angle on a straight line is 180 degrees.

`\begin{gathered} \implies m+k+j=180 \\ m+70+40=180 \\ m=180-110 \\ m=70 \end{gathered}`