Question

Algebra1B CPidentify a solution to the system, explain why it works within the context of the problem and within the graph

Answer 1

We need to identify the solution to the system of inequalities shown below:

`\begin{gathered} x+2y\leq500 \\ 3x\text{ + 4y }\leq1200 \end{gathered}`

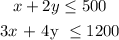
The variable x represents the number of shirts made and the variable y represents the number of pajamas made.

The first inequality means that the amount material used to make the shirts summed with the amount of material used to make the pajamas must be less or equal to 500 yards of cotton. While the second inequation means that the number of hours spent to create the shirts summed with the hours spent to create the pajamas must be less than 1200 hours.

Let's solve the inequality as shown below:

`\begin{gathered} x+2y\leq500 \\ 3x+4y\leq1200 \\ \text{We first n}ed\text{ to transform them in equations:} \\ x+2y=500 \\ 3x+4y=1200 \\ \text{Now we multiply the first equation by -3.} \\ -3x-6y=-1500 \\ 3x+4y=1200 \\ We\text{ can add both equations to cancel one variable} \\ -6y+4y=-1500+1200 \\ -2y=-300 \\ y=(-300)/(-2)=150 \\ \text{Now we n}ed\text{ to replace y on one of the equations to }\det er\min e\text{ the solution:} \\ x+2\cdot150=500 \\ x+300=500 \\ x=500-300=200 \\ \text{The solution is (200, 150). } \end{gathered}`

This means that at most we should fabricate 200 shirts and 150 pajamas. On the graph the solution is represented as below:

The solution works because if we produce 200 shirts and 150 pajamas, we will use exactly the amount of material at our disposal (500 yards of cotton) and it will be done within our time budget (1200 hours).