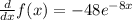Let f(x) = 6exp(-8x).
Using the properties of derivatives, differentiate f(x):
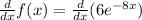
Take the constant factor of 6 out of the derivative:
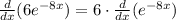
Let u = -8x and rewrite the expression:
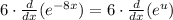
Using the Chain Rule, we know that:
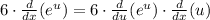
The derivative of the exponential function e^u is again e^u:

Substitute back u = -8x :

Take the constant factor of -8 out of the derivative:
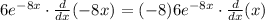
The derivative of x (with respect to x) is 1:

Solve the corresponding products:
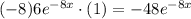
Therefore, the derivative of the function f(x) is given by: