Question

you pick a card at random without getting the first card back you pick a second card at random what is the probability of picking a 4 and then picking a 5 Cards given in the picture: 4, 5, 6, 7

Answer 1

We have to calculate the probability of picking a 4 and then a 5 without replacement.

We can express this as the product of the probabilities of two events:

• The probability of picking a 4

,

• The probability of picking a 5, given that a 4 has been retired from the deck.

We have one card in the deck out of fouor cards that is a "4".

Then, the probability of picking a "4" will be:

`P(4)=(1)/(4)`

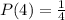
The probability of picking a "5" will be now equal to one card (the number of 5's in the deck) divided by the number of remaining cards (3 cards):

`P(5|4)=(1)/(3)`

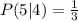
We then calculate the probabilities of this two events happening in sequence as:

`\begin{gathered} P(4,5)=P(4)\cdot P(5|4) \\ P(4,5)=(1)/(4)\cdot(1)/(3)=(1)/(12) \end{gathered}`

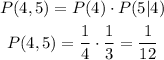
Answer: 1/12