Answer:
Compound interest: A = $1824.98
Simple interest: A = $1800
Step-by-step explanation:
To know the balance after t years for an account that pays with a compounded rate, we can use the following equation:
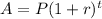
Where P is the initial amount and r is the interest rate.
So, replacing P by $1500, r by 4% or 0.04, and t by 5 years, we get:
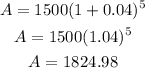
Therefore, in this case, the balance after 5 years is $1824.98
On the other hand, the balance after t years for an account that pays with a simple interest rate can be calculated as:
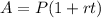
So, replacing P by $1500, r by 0.04, and t by 5 years, we get:
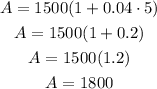
Then, the balance after 5 years is $1800
So, the answers are:
Compound interest: A = $1824.98
Simple interest: A = $1800