Question

Hi, can you help me to solve this exercise please!!

Answer 1

`\cos (\theta)=(4)/(5)`

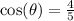
1) In this question, we can notice that theta is in Quadrant IV. In this quadrant, the cosine of theta yields a positive value.

2) So, let's make use of a Pythagorean Identity to find the value of the cosine of theta, given the sine of that same angle:

`\begin{gathered} \sin ^2(\theta)+\cos ^2(\theta)=1 \\ (-(3)/(5))^2+\cos ^2(\theta)=1 \\ (9)/(25)+\cos ^2(\theta)=1 \\ \cos ^2(\theta)=1-(9)/(25) \\ \cos ^2(\theta)=(25)/(25)-(9)/(25) \\ \cos ^2(\theta)=(16)/(25) \\ \sqrt[]{\cos ^2(\theta)}=\sqrt[]{(16)/(25)} \\ \cos (\theta)=(4)/(5) \end{gathered}`

3) Thus the cosine of theta is 4/5 for in Quadrant IV cosine is positive.