Given:
Given that a trigonometric statement.
Required:
To check whether the given statements are true or false`.
Step-by-step explanation:
(1)
Now consider LHS side of the given statement,
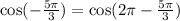
Because adding 2π does not change the value of a trigonometric function.
Now,

Therefore, the statement is false.
(2)
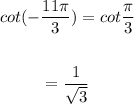
Therefore, the statement is False.
(3)
Remove full rotations of 2π until the angle is between 0 and 2π.

Therefore, the statement is TRUE.
Final Answer:
The first and second statement are FALSE and the third one is TRUE.
.