In order to find the number of different ways the committee can be made, first let's calculate the possibilities for the teachers.
Since we have 8 teachers and need to choose 3, we have a combination of 8 choose 3.
A combination of n choose p is calculated with the formula below:
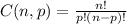
So, for n = 8 and p = 3, we have:

Now, for the students, we have 15 students and need to choose 6, so we have a combination of 15 choose 6:
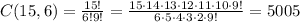
Multiplying both numbers of possibilities, we have the final result:
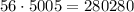
Therefore there are 280,280 different ways of making the committee.