Question

Find the real or imaginary solutions of the following equation by factoring. x^3-64=0Choose the correct answer below.

Answer 1

We want to factor

`x^3-64=0`

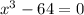
Looking at this, we can tell that (x - 4) or (x + 4) would be one of its factors, since 4 is a factor of 64. So let use check for (x - 4)

So, we will put x = 4 into the equation, we have

`\begin{gathered} x^3-64 \\ 4^3-64 \\ 64-64=0 \end{gathered}`

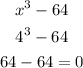
hence (x - 4) is a factor. Dividing the polynomial by (x - 4), we have

`(x^3-64)/(x-4)`

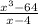
so we got

`x^2+4x+16`

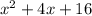
Factorizing the result, we have

`\begin{gathered} x^2+4x+16 \\ We\text{ find the discriminant using } \\ D=b^2-4ac \\ D=4^2-4*1*16 \\ D=16-64 \\ D=-48 \end{gathered}`

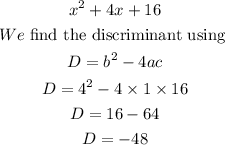
Now we have the discriminant, we use the formula to fin the roots of this equation, we have

`\begin{gathered} x_1=(-b-√(D))/(2a) \\ =(-4-√(-48))/(2*1) \\ =(-4-4√(3)i)/(2) \\ =-2-2√(3)i \end{gathered}`

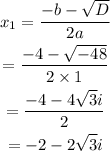
The second root becomes

`\begin{gathered} x_1=(-b+√(D))/(2a) \\ =(-4+√(-48))/(2*1) \\ =(-4+4√(3)i)/(2) \\ =-2+2√(3)i \end{gathered}`

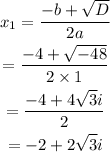
Note that square root of -1 is i

So, comparing to the options, we can see that

The answer is option D