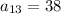We have the following arithmetic sequence:
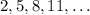
Now, the general n-term of this sequence can be written in the following way:
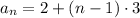
where n takes the following values:
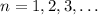
We see that this general term reproduces the sequence about:
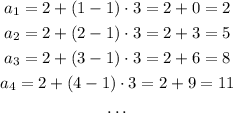
We can find the 13th term of sequence simply replacing n by 13 in the general formula above, we get:

Answer
The 13th term of the sequence is: