Question

6. The table has data about the fate of passengers in the sinking of the Titanic ocean liner inDetermine each of the following: (4 x 2 = 8 marks)(a) P(not surviving first class)(b) P (not surviving in first class and not a man)(c) P (not surviving in second class and not a man)(d) P (not surviving in third class and not a man)(e) What conclusion (s) can you draw based on the above probabilities? Briefly explain youranswer (2 marks)

Answer 1

• (a)P(not surviving | first class)=0.4061.

,

• (b)P (not surviving| in first class and not a man)= 0.0403.

,

• (c)P (not surviving| in second class and not a man)= 0.1121.

,

• (d)P (not surviving in third class and not a man)= 0.1159.

Explanation:

From the given information, the data is totalled in the table below:

(a) P(not surviving | first class)

• The total number of those in First Class = 293

,

• The number of those in First class who died = 114+4+1=119

Therefore:

`P\left(\text{not surviving}|\text{ first class}\right)=(119)/(293)\approx0.4061`

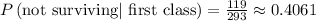
The probability of not surviving given that they are in first class is 0.4061.

(b) P (not surviving| in first class and not a man)

• The number of women and children in first class = 293-(114+55)=124

,

• The number of women and children who died = 4 + 1 =5

`\text{ P \lparen not surviving\mid in first class and not a man\rparen}=(5)/(124)=0.0403`

The probability of not surviving given that they are in first class and not a man is 0.0403.

(c)P (not surviving| in second class and not a man)

• The number of women and children in second class = 268-(139+13)=116

,

• The number of women and children who died = 13+0 = 13

`\text{ P \lparen not surviving\mid in second class and not a man\rparen}=(13)/(116)\approx0.1121`

The probability of not surviving given that they are in second class and not a man is 0.1121.

(d)P (not surviving in third class and not a man)

• The number of women and children who died in third class = 91+55=146

,

• The total number of passengers = 1260

Therefore:

`\text{ P \lparen not surviving in third class and not a man\rparen}=(146)/(1260)\approx0.1159`

The probability of not surviving in third class and not a man is 0.1159.

(e)Of the calculated probabilities, the probability of not surviving given that they are in first class is the highest.