Question

The segment joining Allenville to Batesville is parallel to CD. If you travel through the forest, what is the distance from Allenville to Batesville? What is the distance from Allenville to Farmington? (The vertical angles are right angles.) Allenville Batesville 7.5 mi Farmington 1.2 mi 0.72 mi с 1.4 mi D Allenville to Batesville = mi Allenville to Farmington = mi

Answer 1

First, we will need to find angle D

Using the sine formula

`\frac{\sin\text{ 90}}{1.4}=\frac{\sin \text{ D}}{1.2}`

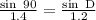
cross multiply

1.2 sin90 = sinD(1.4)

1.2(1) = sin D (1.4)

Divide both-side by 1.4

1.2/1.4 = sin D

0.85714 = sin D

Find the sin⁻' of both-side

sin⁻' (0.85714) = D

58.99 = D

D≈ 59

Let the angle form in Allenville be E

angle D = angle E (alternate angle)

We can now go ahead and find the distance from Allenville to Bastesville using the sine formula

Let x be the distance from Allenville to Bastesville

Hence;

`(\sin90)/(x)=\frac{\sin \text{ 59}}{7.5}`

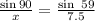
cross-multiply

7.5 sin 90 = x sin59

7.5(1) = x sin 59

Divide both-side of the equation by sin 59

7.5 / sin 59 = x

8.7498 = x

x≈ 8.75

Therefore, the distance from Allenville to Basteville is 8.75 miles

To find the distance from Allenville to Farmington, we can simply use pythagoras theorem, since it is a right-triangle

Let the distance from Allenville to Farmington be y

Using Pythagoras theorem;

opposite² + adjacent² = hypotenuse²

y² + 7.5² = 8.75²

y² + 56.25 = 76.5625

subtract 56.25 from both-side of the equation

y² = 76.5625 - 56.25

y² =20.3125

Take the square root of both-side

y = 4.50693

y≈ 4.5

Therefore, the distance from Allenville to Farmington is 4.5 mile