Question

I need help with the EC question

Answer 1

all values of x between 0 and 2 pi are 0.12, 1.45, 3.24, and 4.59.

In degrees, this is 6.88, 83.1, 185.6 and 262.98 degrees.

Explanation:

First we realize that

`\sin 2x=2\sin x\cos x`

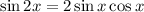
therefore, the equation

`(2\sin x\cos x)^2+4\sin 2x=1`

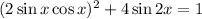
becomes

`(\sin 2x)^2+4\sin 2x=1`

We can complete the square here by adding 4 to both sides. This gives

`(\sin 2x)^2+4\sin 2x+4=5`
`(\sin 2x+2)^2=5`

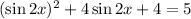
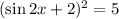
taking the square root of both sides gives

`\sin 2x+2=\sqrt[]{5}`

Subtracting 2 from both sides gives

`\sin 2x=\sqrt[]{5}-2`

Finally, taking the inverse of both sides gives

`2x=\sin ^(-1)\lbrack\sqrt[]{5}-2\rbrack`
`x=\frac{\sin ^(-1)\lbrack\sqrt[]{5}-2\rbrack}{2}`

The first two values of the inverse function are

`\begin{gathered} \frac{\sin ^(-1)\lbrack\sqrt[]{5}-2\rbrack}{2}=0.12 \\ \end{gathered}`
`\frac{\sin^(-1)\lbrack\sqrt[]{5}-2\rbrack}{2}=1.45`
`\frac{\sin^(-1)\lbrack\sqrt[]{5}-2\rbrack}{2}=3.24`

`\frac{\sin^(-1)\lbrack\sqrt[]{5}-2\rbrack}{2}=4.59`

Hence, all values of x between 0 and 2 pi are 0.12, 1.45, 3.24, and 4.59.

In degrees, this is 6.88, 83.1, 185.6 and 262.98 degrees.