Question

Balance these reactions and indicate the type of reaction the equation represents: Ba(C2H3O2)2 + Na3PO4 → Ba3(PO4)2 + NaC2H3O2

Answer 1

Let's rewrite the unbalanced equation:

`Ba(C_2H_3O_2)_2+Na_3PO_4\to Ba_3(PO_4)_2+NaC_2H_3O_2`

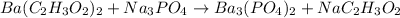
For the equation to be balanced, we need all the atoms to have equal number in each side.

However, we have som unchanged groups: C₂H₃O₂⁻ and PO₄³⁻ are unmodified, so we can consider them as one thing.

So, starting from Ba, we see that we have 1 on the left side and 3 on the right side, so let's start by adding a coefficient 3 to the left side so that Ba gets balanced:

`3Ba(C_2H_3O_2)_2+Na_3PO_4\to Ba_3(PO_4)_2+NaC_2H_3O_2`

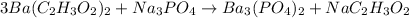
Now, the group C₂H₃O₂⁻ appear 6 times in the left side and only once on the right side. We can fix that by adding a coefficient 6 to NaC₂H₃O₂:

`3Ba(C_2H_3O_2)_2+Na_3PO_4\to Ba_3(PO_4)_2+6NaC_2H_3O_2`

Now, we can look to Na: we have 3 on the left side and 6 on the right side. So, we can add a coefficient 2 on Na₃PO₄:

`3Ba(C_2H_3O_2)_2+2Na_3PO_4\to Ba_3(PO_4)_2+6NaC_2H_3O_2`

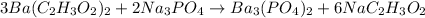
Now we check wether PO₄³⁻ is balanced: it appears twice on the left side and twice on the right side, so it is balanced.

Thus, the balanced equation is:

`3Ba(C_2H_3O_2)_2+2Na_3PO_4\to Ba_3(PO_4)_2+6NaC_2H_3O_2`

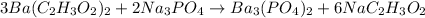
Also, we can see that the group C₂H₃O₂⁻ went from Ba to Na, and that the group PO₄³⁻ went from Ba to Na, that is both groups were displaced.

Thus, this is a double-displacement reaction.