Question

Algebra1B CPcreate a function that represents the path traveled by the kickball

Answer 1

Given that the ball travels 10 ft horizontally, then the maximum is reached at half of this distance, that is 5 ft. This means that the parabola has a maximum at (5, 25).

The equation of a parabola in vertex form is:

`y=a(x-h)^2+k`

where (h, k) is the vertex.

Substituting with the vertex (5, 25) and the point (0,0) we get:

`\begin{gathered} 0=a(0-5)^2+25 \\ 0=a\cdot25+25 \\ -25=a\cdot25 \\ -(25)/(25)=a \\ -1=a \end{gathered}`

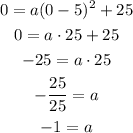
And the function that models the path traveled by the ball is:

`y=-(x-5)^2+25`

where y is the vertical distance, or height, in ft, and x is the horizontal distance, also in ft.