Question

Solve the equation: √ x + 83 = x + 11 x =

Answer 1

We have to solve the following expression:

`\begin{gathered} √(x+83)=x+11 \\ x+83=(x+11)^2 \\ x+83=x^2+2*11*x+11^2 \\ x+83=x^2+22x+121 \\ 0=x^2+22x+121-x-83 \\ 0=x^2+21x+38 \end{gathered}`

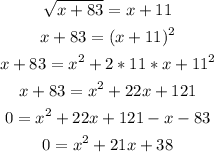
We now have to apply the quadratic equation to find the possible solutions:

`\begin{gathered} x=(-21\pm√(21^2-4*1*38))/(2*1) \\ x=(-21\pm√(441-152))/(2) \\ x=(-21\pm√(289))/(2) \\ x=(-21\pm17)/(2) \\ =>x_1=(-21-17)/(2)=-(38)/(2)=-19 \\ =>x_2=(-21+17)/(2)=-(4)/(2)=-2 \end{gathered}`

We have found two possible solutions: x = -19 and x = -2.

One of this solution is valid and the other is not.

We can check this knowing that the square root will always (unless expressed the contrary with a minus sign) be a positive number.

This means that is √(x+83) is positive, so has to be x + 11.

The first solution is x = -19, so:

`x+11=-19+11=-8<0`

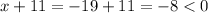
Then, this solution is not the correct one.

We test the other solution (x = -2) and get:

`x+11=-2+11=9>0`

This solution is the correct one.

Answer: x = -2.