hello
from the question given, we can easily find the value of angle 5
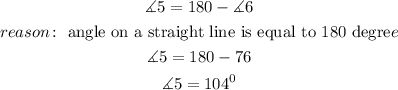
having found the value of angle 5, it is easily relatable to angle 3 because they are alternating angles to each other
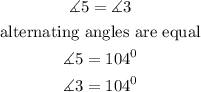
from the calculations above, the value of angle 3 is equal to 104 degrees
it is an alternate interior angle theorem