Question

I need help with this whole sheet,im horrible at geometry.I haven’t learned anything on this since the beginning of the subject

Answer 1

Step 1:

For Question No 1, we are given the following:

Recall that :

The opposite sides of a parallelogram are equal and parallel to each other.

This means that:

`\begin{gathered} XY\text{ = WZ} \\ \text{and } \\ XW\text{ = YZ} \end{gathered}`
`\begin{gathered} \text{where XY = }3a\text{ - 4} \\ WZ\text{ = a+ 2} \end{gathered}`

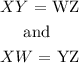
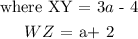
This means that:

`\begin{gathered} \text{3a - 4 = a + 2} \\ \text{collecting like terms, we have that:} \\ 3a\text{ - a = 2+ 4} \\ 2a\text{ = 6} \\ \text{Divide both sides by 2, we have that:} \\ \text{a =}(6)/(2)=\text{ 3} \\ \text{Hence, the value of a = 3} \end{gathered}`

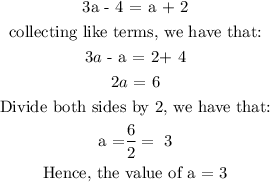
On the other hand,

`\begin{gathered} XW\text{ = YZ} \\ \text{where XW = b+ 1} \\ \text{and } \\ YZ\text{ = 2b} \\ \text{This means that:} \\ b+\text{ 1= 2b} \\ \text{collecting like terms, we have that:} \\ 1\text{ = 2b - b} \\ b\text{ = 1} \\ \text{Hence, the value of b = 1} \end{gathered}`

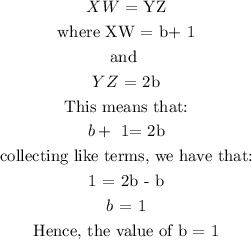
CONCLUSION:

The value of a = 3

The value of b = 1