Question

The equation x^2+y^2=25 defines a circle with a center at the origin of and radius of 5. The line y=x-1 passes for through the circle. Using the substitution method, find the point(s) at which the circle and the line intersect.

Answer 1

(-3,-4) and (4,3)

Step-by-step explanation:

The equations of the circle and the line are given below:

`\begin{gathered} x^2+y^2=25 \\ y=x-1 \end{gathered}`

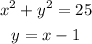
Substitute the second equation into the first:

`\begin{gathered} x^2+y^2=25 \\ x^2+(x-1)^2=25 \\ x^2+(x-1)(x-1)=25 \\ x^2+x^2-x-x+1=25 \\ 2x^2-2x+1-25=0 \\ 2x^2-2x-24=0 \end{gathered}`

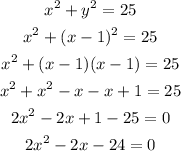
Solve the equation for x:

`\begin{gathered} 2(x^2-x-12)=0 \\ x^2-4x+3x-12=0 \\ x(x-4)+3(x-4)=0 \\ (x+3)(x-4)=0 \\ x=-3\text{ or }x=4 \end{gathered}`

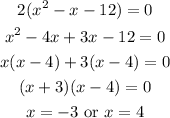
Next, find the corresponding values of y for each x:

When x=-3

`\begin{gathered} y=-3-1 \\ y=-4 \\ \implies(-3,-4) \end{gathered}`

When x=4

`\begin{gathered} y=4-1 \\ y=3 \\ \implies(4,3) \end{gathered}`

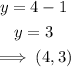
The points at which the circle and the line intersect are (-3,-4) and (4,3).