Question

Dalco Manufacturing estimates that its weekly profit, P, in hundreds of dollars, can be approximated by theformula P = -4x² + 8x + 4, where x is the number of units produced per week, in thousands.-a. How many units should the company produce per week to earn the maximum profit?Find the maximum weekly profit.a. 1,000 units; $300b. 1,000 units; $800c. 4,000 units; $2800d. 2,000 units; $600

Answer 1

We must find the maximum of the following function:

`P(x)=-4x^2+8x+4.`

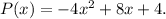
To find the maximum, we equal to zero the first derivative of P(x):

`P^(\prime)(x)=-4\cdot2x+8=0,`

and then we solve for x:

`\begin{gathered} -4\cdot2x+8=0, \\ -8x+8=0, \\ 8x=8, \\ x=(8)/(8)=1. \end{gathered}`

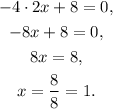
Now, we evaluate the function for x = 1, we get:

`P(1)=-4\cdot1^2+8\cdot1+4=8.`

From the statement we know that:

• x is the number of units produced per week, in thousands,

,

• P(x) is the weekly profit, in hundreds of dollars.

So the maximum is reached for 1,000 units and the profit is $800 in that case.

Answer

b. 1,000 units; $800