Question

I need help with this practice problem On the top of the picture is the instructions

Answer 1

Recall that:

The terminal ray of the angle θ drawn in standard position lie in:

1) Quadrant I if:

`0<\theta<(\pi)/(2)\text{.}`

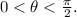
2) Quadrant II if:

`(\pi)/(2)<\theta<\pi\text{.}`

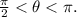
3) Quadrant III if:

`\pi<\theta<(3\pi)/(2)\text{.}`

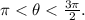
4) Quadrant IV if:

`(3\pi)/(2)<\theta<2\pi\text{.}`

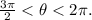
Also, recall that θ and θ+2πn (with n an integer) are equivalent angles.

Now, notice that:

`\begin{gathered} (\pi)/(2)<(3\pi)/(4)<\pi, \\ (57\pi)/(8)\rightarrow(9)/(8)\pi\text{ and }(\pi)/(2)<(9\pi)/(8)<\pi, \\ (13)/(6)\pi\rightarrow(1)/(6)\pi\text{ and }0<(\pi)/(6)<(\pi)/(2), \\ -(35\pi)/(4)\rightarrow(5)/(4)\pi\text{ and }\pi<(5\pi)/(4)<(3\pi)/(2), \\ -(5)/(6)\pi\rightarrow(7\pi)/(6)\text{ and }\pi<(7\pi)/(6)<(3\pi)/(2), \\ -(5)/(11)\pi\rightarrow(17)/(11)\pi\text{ and }(3\pi)/(2)<(17\pi)/(11)<2\pi\text{.} \end{gathered}`

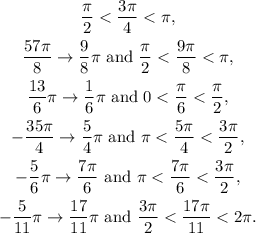
Therefore the fulfilled table is:

Answer: