We are given a set of numbers and we are asked to organize them from least to greatest. To do that we need to have into account that given two negative numbers the greater will be the one closer to zero, and given two positive numbers the greater will be the one further away from zero. Therefore, the number should be organized as:
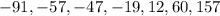
The same procedure can be used to answer question 32.