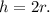From geometry, we know that:
• the volume of a sphere of radius r is:
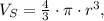
• the volume of a cylinder of radius r and heigth h is:
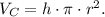
If the volume of the sphere (Vs) is 2/3 the volume of the cylinder (Vc), we have:
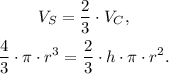
Solving for h, we find that:
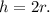
We have found that the height of the cylinder is two times its radius.
Answer
• We have a sphere and cylinder with the same radius.
,
• We know that the volume of the sphere is
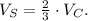
• By replacing the formulas of each volume, we find that the heigh of the cylinder is: