(a)
The formula for future value of an amount of money is given by >>>
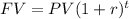
Where
FV is the future value
PV is the present value
r is the rate of interest per period, in decimal
t is the time period
Given,
PV = 8806.54
Rate of interest is 6% annual, so semi annual compounding means that r = 6%/2 = 3% = 0.03
In 7 years, there are 7 x 2 = 14 compoundings, since semi annual compounding. We use t = 14
Plugging all the information, we get:
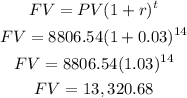
The future value at semi-annual compounding is $13,320.68
The interest earned is about $13,320.68 - $8806.54 = $4514.14
(b)
When we are continuously compounding, we use a slightly different formula. That is
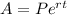
Where
A is the future value
P is the initial amount
r is the rate of interest
t is the time period
We know,
P = 8806.54
r = 6% = 0.06
t = 7
So, plugging in gives us,
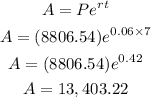
The future value at continuous compounding is $13,403.22
The interest earned is about $13,403.22 - $8806.54 = $4596.68