We are asked to find the conditional probability that the student is a male given that it's a senior.
Recall that the conditional probability is given by
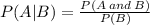
P(A | B) means that the probability of event A given that event B has already occurred.
Applying it to the given situation,
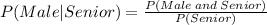
The probability P(Male and Senior) is given by
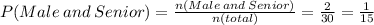
Where n(Male and Senior) is the intersection of the row "Male" and the column "Senior" that is 2
n(total) is the grand total of all the students.
Grand total = 4+3+6+4+2+6+2+3 = 30
The probability P(Senior) is given by
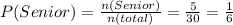
Where n(Senior) is the column total of the column "Senior" that is (2 + 3 = 5)
n(total) is the grand total of all the students.
Finally, the probability that the student is a male given that it's a senior is
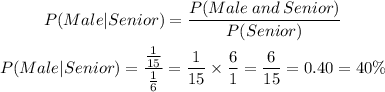
Therefore, the probability that the student is a male given that it's a senior is 40%