Question

Element X is a radio isotope with half lives of 11 yrs. The initial mass of element x is 60 grams. How much to the nearest tenth of the element remains after 25 yrs?

Answer 1

We are given that a radio isotope has an initial mass of 60 grams and a half-life of 11 years. The mass of the isotope with respect to time can be modeled using the following exponential function:

`M=m_0e^(kt)`

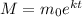
Where:

`\begin{gathered} M=\text{ mass} \\ m_0=\text{ initial mass} \\ k=\text{ constant} \\ t=\text{ time} \end{gathered}`

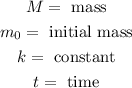
Now, since we are given that the half-life is 11 years this means that the mass will be half of the initial mass when "t = 11 years". We can use this fact to calculate the value of "k". Substituting half the initial mass we get:

`(m_0)/(2)=m_0e^{k(11\text{year)}}`

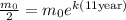
Now, we may cancel the initial mass:

`(1)/(2)=e^{k(11\text{years)}}`

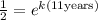
Now, we solve for "k". To do that we will take natural logarithm to both sides:

`\ln (1)/(2)=\ln e^{k(11\text{years)}}`

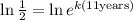
Now, we use the following property of logarithms:

`\ln x^y=y\ln x`

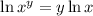
Applying the property we get:

`\ln (1)/(2)=k(11years)\ln e^{}`

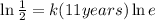
We have that:

`\ln e=1`

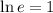
Therefore:

`\ln (1)/(2)=k(11years)`

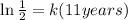
Now, we divide both sides by 11:

`(1)/(11)\ln (1)/(2)=k`

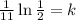
Solving the operations:

`-0.063=k`

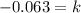
Now, we substitute in the formula for the mass:

`M=60e^(-0.063t)`

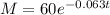
Now, to determine the value of the mass after 25 years we substitute the value "t = 25", we get:

`M=60e^(-0.063(25))`

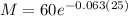
Solving the operations:

`M=12.4`

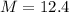
Therefore, the mass after 25 years is 12.4 grams.