Since triangle STU is a reduction of the triangle PQR, their corresponding sides are related by the equation:
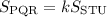
Where K is a constant, and that constant is the same whichever pair of corresponding sides we choose.
Let's take the PQR side, its length is given by:
![\begin{gathered} P=(-8,4),R=(-4,-2) \\ \Rightarrow d_(PR)=\sqrt[]{(-8+4)^2+(4+2)^2}=\sqrt[]{16+36}=\sqrt[]{52} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/44vjpl28hipftgjaxvb2vzddjmnqnzntr9.png)
On the other hand, the length of the SU side is:
![\begin{gathered} S=(-2,1),U\approx(-1,-1) \\ \Rightarrow d_(SU)\approx\sqrt[]{(-2+1)^2+(1+1)^2}=\sqrt[]{1+4}=\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/iu0htpg412alp8n5tmnansx0fpr7l97rt6.png)
Then, we need to find the value of c in the equation
![\begin{gathered} d_(PR)=c\cdot d_(SU) \\ \Rightarrow c=(d_(PR))/(d_(SU))\approx\sqrt[]{(52)/(5)}=\sqrt[]{10.4}=3.22490\ldots \\ \Rightarrow c\approx3.225 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/muam30q667pm2sc37b7etbwg5p1ihhal1m.png)
Then, as STU is the reduction of PQR, the answer is 1/c, which is:
![\begin{gathered} (1)/(c)\approx\frac{1}{\sqrt[]{10.4}}=0.310087 \\ \Rightarrow(1)/(c)\approx0.31 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q9atx4btv9pxk62oamdjyoqk23b847skzf.png)
The reduction factor is approximately 0.31. For a better result, we need to know with more certainty the coordinates of U