Question

Properties of chords. don’t take forever answering. all i care about is the steps & the answer.

Answer 1

Let us analyze the diagram.

OB = OE

Since OB and OE are both perpendicular bisectors of AC and FD respectively, it follows that

AC = FD

Hence, we can equate the two values to solve for x.

`-5x+13=4x-5`

Collecting like terms,

`\begin{gathered} -5x-4x=-5-13 \\ -9x=-18 \\ x=2 \end{gathered}`

To find AC, we will put the value of x into the expression for AC.

Hence,

`\begin{gathered} AC=-5x+13 \\ AC=-5(2)+13 \\ AC=-10+13 \\ AC=3 \end{gathered}`

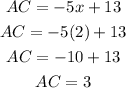
Therefore, the value of AC is 3.