Question

Four different linear functions are represented below.Part A: Which function has the graph with a y-intercept closest to 0? Part B: which function has the graph with the greatest y-intercept?Part C: which functions have graphs with slopes less than 4? Check all that apply

Answer 1

We have here four linear functions, and we have to compare the slopes of them as well as their y-intercept. For this, it is important to remember the general equation for the line in the slope-intercept form:

`y=mx+b`

Where

• m is the slope of the line

,

• b is the y-intercept of the line (0, b)

The y-intercept is the point where the line passes through the y-axis, and at this point, we have that x = 0.

Finding the slopes and the y-intercept for the four functions

Function 1

We have in this case that the function passes through the points:

• (0, 5), (1, 1)

We can find the equation of this line using the two-point form of the line equation:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

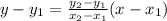
Using the points above, we can label them as follows:

• (0, 5) ---> x1 = 0, y1 = 5

,

• (1, 1) ---> x2 = 1, y2 = 1

Then we have:

`\begin{gathered} y-5_{}=\frac{1_{}-5}{1-0_{}}(x-0_{}) \\ y-5=-(4)/(1)x \\ y-5=-4x \\ y=-4x+5 \end{gathered}`

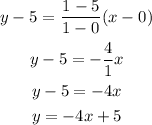
Therefore, the slope for this line is m = -4, and the y-intercept is (0, 5).

Function 2

For Function 2 we need to do the same procedure as before. We have to select two points of the function to find its equation:

We can select the following points: (0, 1), (1, 6).

Then we can proceed as we did in the previous part:

• (0, 1) ---> x1 = 0, y1 = 1

,

• (1, 6) ---> x2 = 1, y2 = 6

`\begin{gathered} y-1_{}=\frac{6_{}-1_{}}{1-0_{}}(x-0) \\ y-1=5x \\ y=5x+1 \end{gathered}`

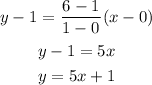
Therefore, the slope in Function 2 is 5, m = 5, and the y-intercept is (0, 1).

Function 3

We can see that Function 3 has already its line equation in slope-intercept form:

`y=-x-2`

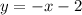
Then the slope for Function 3 is m = -1, and its y-intercept is (0, -2).

Function

From the question, we have: