Question

Why are the triangles similar? Choose the correct answer below.

Answer 1

Given:

In a larger right triangle,

Base, 28ft

Height, x

In a smaller right triangle,

Base, 8ft

Height, 5ft 6inches

In foot,

`\begin{gathered} 5+6((1)/(12))=5+0.5[Since,1\text{ inches =}(1)/(12)foot] \\ =5.5ft \end{gathered}`

To find:

The similarity postulate and the value of x

Step-by-step explanation:

From the diagram, we observe that,

There is a pair of congruent right angles and a pair of congruent angles.

Therefore, by using the AA postulate,

The given two triangles are similar triangles.

So, the corresponding sides are proportional.

Therefore, we write

`\begin{gathered} (x)/(5.5)=(28)/(8) \\ x=(28*5.5)/(8) \\ x=19.25ft \end{gathered}`

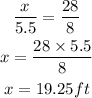
Therefore, the value of x is 19.25 ft.

Final answer: Option C

There is a pair of congruent right angles and a pair of congruent angles. so the triangles are similar by the AA postulate.

The value of x is 19.25 ft.