Question

Solve the following system:2x-6y=-12x+2y=14

Answer 1

We can solve this system by elimination method.

If we multiply by -2 the second equation, we have

`-2x-4y=-28`

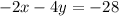
Then, we need to solve the following equivalent system:

`\begin{gathered} 2x-6y=-12 \\ -2x-4y=-28 \end{gathered}`

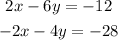
Now, we can see that if we add both equations, we obtain

`-6y-4y=-12-28`

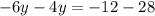
because 2x-2x=0. Then, we have

`\begin{gathered} -10y=-40 \\ y=(-40)/(-10) \\ y=4 \end{gathered}`

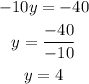
Now, we can substitute this result into the first equation. It yields,

`2x-6(4)=-12`

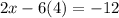
which gives

`\begin{gathered} 2x-24=-12 \\ 2x=-12+24 \\ 2x=12 \\ x=(12)/(2) \\ x=6 \end{gathered}`

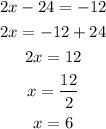
Therefore, the solution is x=6 and y=4.